Electric Circuit

Electric Current

Electric current is the rate of charge flow past a given point in an electric circuit, measured in Coulombs/second which is named Amperes. In most DC electric circuits, it can be assumed that the resistance to current flow is a constant so that the current in the circuit is related to voltage and resistance by Ohm's law. The standard abbreviations for the units are 1 A = 1C/s.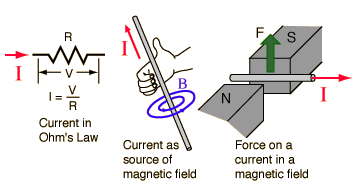

Ohm's Law

For many conductors of electricity, the electric current which will flow through them is directly proportional to the voltage applied to them. When a microscopic view of Ohm's law is taken, it is found to depend upon the fact that the drift velocity of charges through the material is proportional to the electric field in the conductor. The ratio of voltage to current is called the resistance, and if the ratio is constant over a wide range of voltages, the material is said to be an "ohmic" material. If the material can be characterized by such a resistance, then the current can be predicted from the relationship: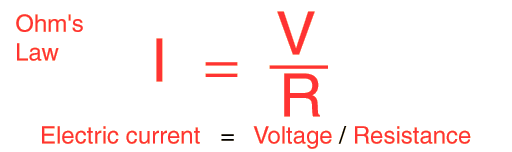

Data can be entered into any of the boxes below. Specifying any two of the quantities determines the third. After you have entered values for two, click on the text representing to third in the active illustration above to calculate its value. 

Voltage

Voltage is electric potential energy per unit charge, measured in joules per coulomb ( = volts). It is often referred to as "electric potential", which then must be distinguished from electric potential energy by noting that the "potential" is a "per-unit-charge" quantity. Like mechanical potential energy, the zero of potential can be chosen at any point, so the difference in voltage is the quantity which is physically meaningful. The difference in voltage measured when moving from point A to point B is equal to the work which would have to be done, per unit charge, against the electric field to move the charge from A to B.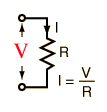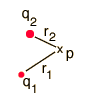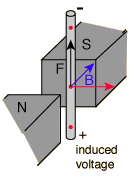

Used to calculate current in Ohm's law.	Used to express conservation of energy around a circuit in the voltage law.	Used to calculate the potential from a distribution of charges.	Is generated by moving a wire in a magnetic field.

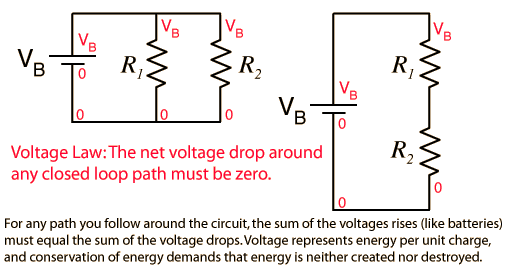
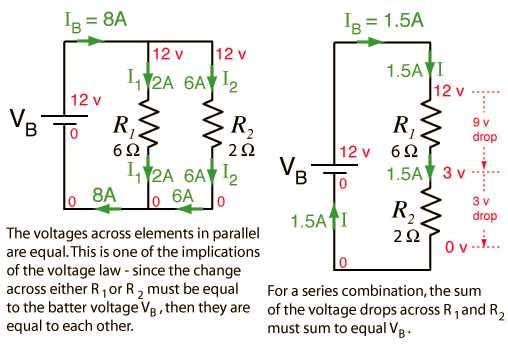
Voltage Law

The voltage changes around any closed loop must sum to zero. No matter what path you take through an electric circuit, if you return to your starting point you must measure the same voltage, constraining the net change around the loop to be zero. Since voltage is electric potential energy per unit charge, the voltage law can be seen to be a consequence of conservation of energy.
The voltage law has great practical utility in the analysis of electric circuits. It is used in conjunction with the current law in many circuit analysis tasks.
The voltage law is one of the main tools for the analysis of electric circuits, along with Ohm's Law, the current law and the power relationship. Applying the voltage law to the above circuits along with Ohm's law and the rules for combining resistors gives the numbers shown below. The determining of the voltages and currents associated with a particular circuit along with the power allows you to completely describe the electrical state of a direct current circuit.